자바스크립트의 Math.random()은 0과 1 사이의 난수를 생성하는 랜덤 함수입니다. 즉, 0과 같거나 크고 1 보다 작은 값을 리턴합니다. (0 <= x < 1)
다른 범위의 숫자가 필요한 경우 간단한 수학을 사용하여 원하는 범위의 값을 얻을 수 있습니다.
참고로 이 메소드는 암호학적으로 안전한 랜덤 값을 생성하지 않습니다.
보안과 관련된 용도로 사용할 경우 Web Crypto API의 window.crypto.getRandomValues() 메소드를 사용하기 바랍니다.
Table of Contents
랜덤 숫자 얻기
실제 사용할 수 있는 사례 중 가장 간단한 예제로는 지정된 범위 내에서 랜덤 값을 생성하는 것 입니다.
특정 범위 내의 값을 얻는 공식은 Math.random() 메소드의 결과 값에 원하는 범위의 최대 값과 최소 값의 차를 곱하고 거기에 최소 값을 더하면 됩니다.
다음의 예제를 개발자 도구에서 확인해 보겠습니다:
const randomNumberInRange = (min, max) => Math.random() * (max - min) + min;
randomNumberInRange(2, 10);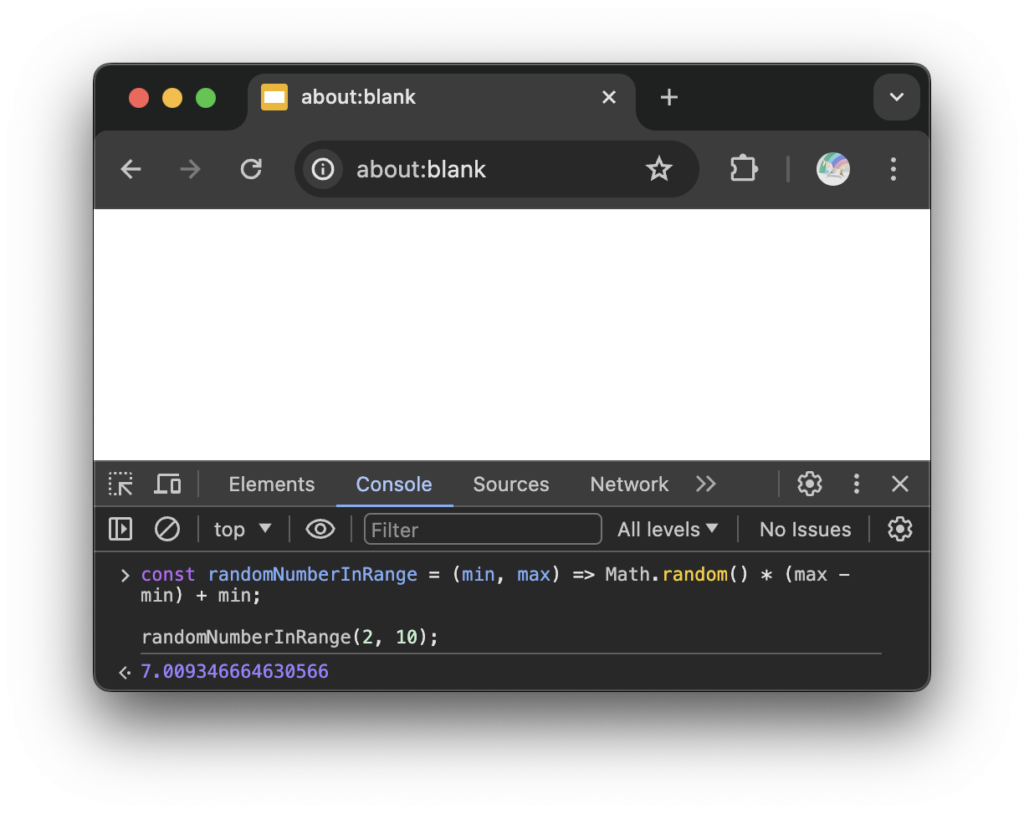
범위 공식에 의해 인라인 함수를 만들고 함수의 매개변수로 최대, 최소 값을 전달하면 최소 값 보다 크거나 같고 최대 값 보다 작은 범위 내의 값을 얻을 수 있습니다.
즉, 최소 값 <= x < 최대 값 형태의 난수를 얻을 수 있습니다.
랜덤 정수 얻기
앞 섹션의 범위 생성 공식에서 한 단계만 추가하면 정수 값을 결과로 리턴할 수 있습니다.
소수점 값에서 정수 값을 얻으려면 Math.floor() 메소드를 사용하면 됩니다.
const randomIntegerInRange = (min, max) => Math.floor(Math.random() * (max - min)) + min;
randomIntegerInRange(0, 5);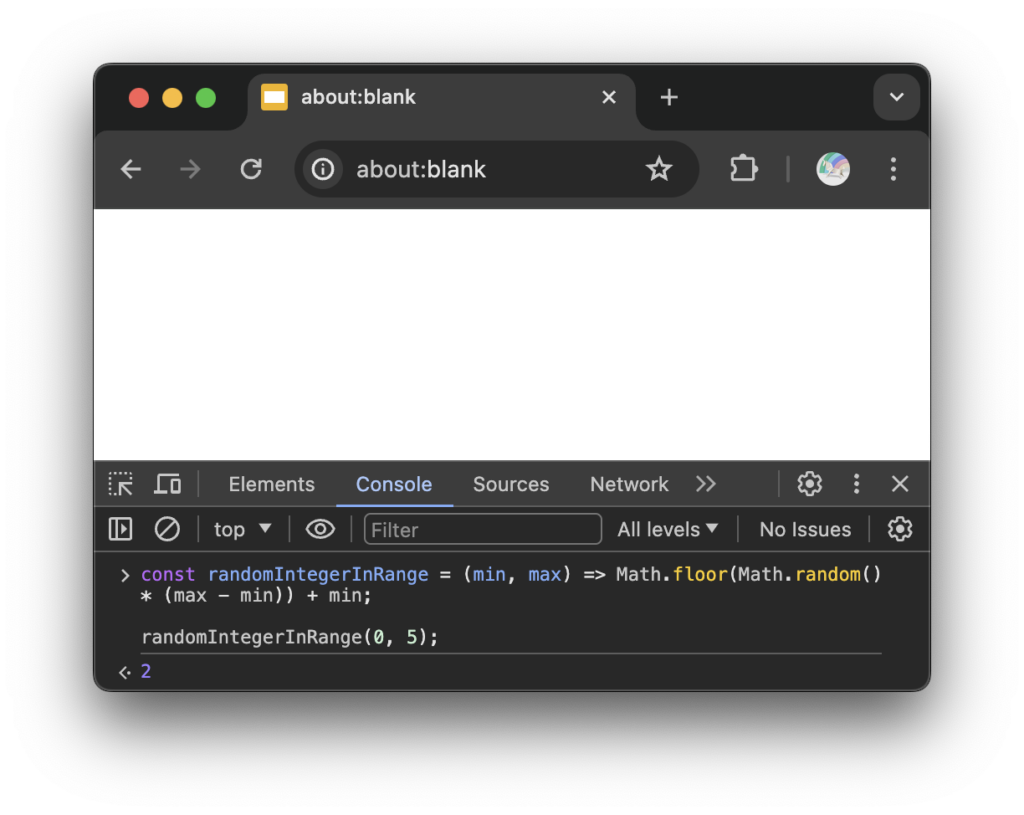
위의 예제에서는 앞 섹션의 범위 내의 값 생성 공식에 Math.floor() 메소드를 추가했습니다.
이렇게 하면 소수점 값으로 된 결과를 정수로 바꿀 수 있습니다.
별다른 추가 공식은 없으므로 범위는 여전히 최소 값 <= x < 최대 값 형태가 됩니다.
이를 응용해 문자열의 인덱스를 랜덤으로 뽑아내면 임의의 문자열을 얻을 수도 있습니다.
가우시안 랜덤 숫자
마지막으로 가우시안(정규 분포) 랜덤 숫자를 얻으려면, 가우스 분포(Gauss Distribution) 생성을 위해 Box-Muller transform을 사용할 수 있습니다.
const randomGauss = () => {
const theta = 2 * Math.PI * Math.random();
const rho = Math.sqrt(-2 * Math.log(1 - Math.random()));
return (rho * Math.cos(theta)) / 10.0 + 0.5;
};
randomGauss();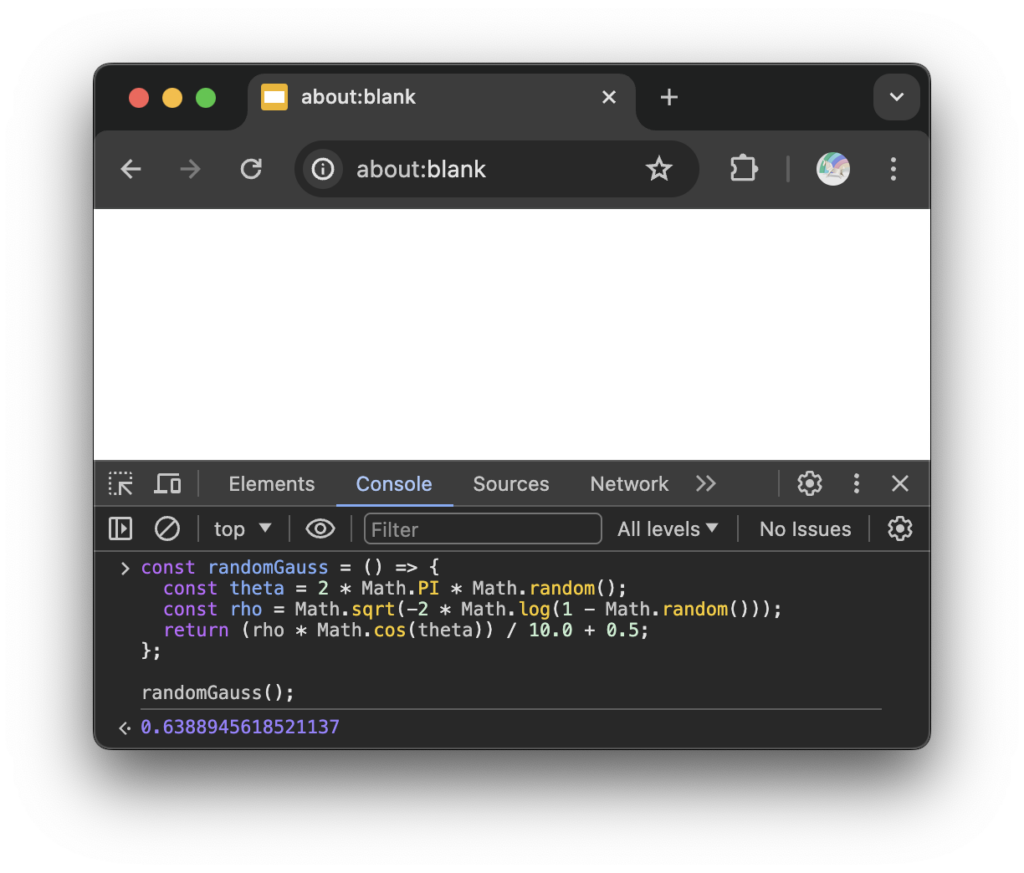
정규 분포는 산술 평균 근처에 값이 더 많이 모여있는 분포를 이르는 말로 가우스 분포 라고도 합니다.
위의 예제와 같이 box-muller 변환법 공식을 사용하여 일반적인 random() 메소드의 결과 값이 아닌 정규 분포를 따르는 값을 생성할 수 있습니다.
randomGauss() 함수를 아주 많이 실행해 결과 값의 분포를 확인해 보면 정규 분포 그래프와 비슷하게 값이 생성되는 것을 확인할 수 있습니다.
정리
이 포스트에서는 자바스크립트의 Math.random() 메소드를 사용하여 특정 범위 내의 값을 생성하는 방법을 알아봤습니다.
먼저 가장 간단한 범위 내의 소수점 숫자를 생성하는 방법을 알아봤고, 생성된 소수점 숫자에 Math.floor() 메소드를 통해 정수화 하는 방법도 알아봤습니다.
마지막으로 정규 분포를 따르는 랜덤 숫자 생성 방법도 알아봤습니다.
random() 메소드는 0 ~ 1 사이의 숫자를 생성해 주지만 이 값에 여러 공식을 사용하여 다양한 결과를 만들 수 있습니다.